티스토리 뷰
https://www.acmicpc.net/problem/1208
1208번: 부분수열의 합 2
첫째 줄에 정수의 개수를 나타내는 N과 정수 S가 주어진다. (1 ≤ N ≤ 40, |S| ≤ 1,000,000) 둘째 줄에 N개의 정수가 빈 칸을 사이에 두고 주어진다. 주어지는 정수의 절댓값은 100,000을 넘지 않는다.
www.acmicpc.net
부분수열의 합 1과 다른 점은, N의 제한이 [1, 40]이라는 것이다. 때문에 N = 40일 경우 $2^{n}=10^{12}$라는 어마어마한 값이 나온다...
수열을 반으로 쪼개 각 부분수열의 합을 구한다음, 투 포인터를 사용해 두 수열의 합이 S가 나올 수 있는 경우를 돌아보면 된다.

N과 S는 각각 6과 4라고 가정할 때, 구한 두 부분수열의 합을 정렬한 다음 하나는 왼쪽, 하나는 오른쪽에서 시작한다.
현재 두 포인터가 가리키고 있는 값의 합(0 + 6 = 6)이 4보다 작으므로, 값을 작게 만들기 위해 Right 포인터를 한 칸 왼쪽으로 보낸다.

두 포인터가 가리키고 있는 값의 합(0 + 5 = 5)이 4보다 작으므로, 역시 Right 포인터를 한 칸 왼쪽으로 보낸다.

두 포인터가 가리키고 있는 값의 합(0 + 4 = 4)이 4와 같다!!
가능한 경우의 수를 하나 늘리고, 두 포인터를 각각 한 칸씩 이동시킨다.

역시 두 포인터가 가리키고 있는 값의 합(1+3 = 4)이 4와 같다.
하지만, 여기서는 단순히 가능한 경우의 수를 하나 늘리고 두 포인터를 한 칸씩 이동시켜주지 않는다.

연속된 위치에 같은 조합으로 4가 되는 경우가 또 있기 때문에, 가능한 경우의 수를 2 * 2 = 4개 늘려준다.

만약 첫번째 수열의 4번째 원소의 값이 2가 아닌 1이였다면, 각각의 1마다 2개의 3으로 4를 만들 수 있으니, 가능한 경우의 수가 3 * 2 = 6개 늘어난다.
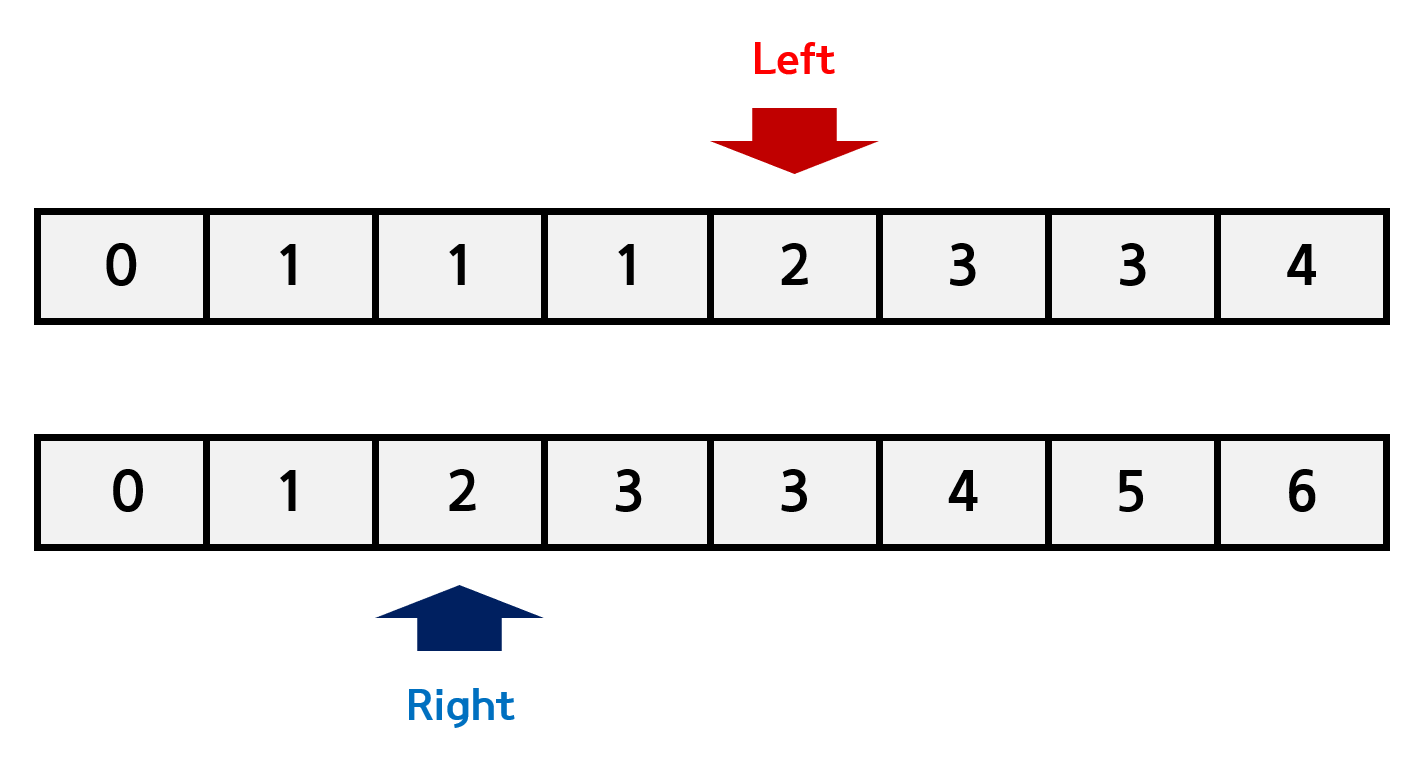
값을 계산한 것을 제외하고 포인터를 다시 옮겨준 다음, 포인터가 한 쪽 끝에 도달할 때까지 위 과정을 반복하면 된다.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
int n, s;
std::cin >> n >> s;
std::vector<int> a1, a2;
for (int i = 0; i < n / 2; ++i) {
int a; std::cin >> a;
a1.push_back(a);
}
for (int i = n / 2; i < n; ++i) {
int a; std::cin >> a;
a2.push_back(a);
}
std::vector<int> set1, set2;
int s1 = a1.size(), s2 = a2.size();
for (int i = 0; i < (1 << s1); ++i) {
int sum = 0;
for (int j = 0; j < s1; ++j) {
if (i & (1 << j)) {
sum += a1[j];
}
}
set1.push_back(sum);
}
for (int i = 0; i < (1 << s2); ++i) {
int sum = 0;
for (int j = 0; j < s2; ++j) {
if (i & (1 << j)) {
sum += a2[j];
}
}
set2.push_back(sum);
}
std::sort(set1.begin(), set1.end());
std::sort(set2.begin(), set2.end());
int left = 0, right = set2.size() - 1;
long long ans = 0;
s1 = set1.size(), s2 = set2.size();
while (left < s1 && right >= 0) {
int sum = set1[left] + set2[right];
if (sum < s) {
++left;
}
else if (sum > s) {
--right;
}
else {
long long c1 = 1, c2 = 1;
for (int i = left + 1; i < s1; ++i, ++c1) {
if (set1[left] != set1[i]) break;
}
for (int i = right - 1; i >= 0; --i, ++c2) {
if (set2[right] != set2[i]) break;
}
ans += c1 * c2;
left += c1;
right -= c2;
}
}
if (s == 0) --ans;
std::cout << ans;
return 0;
}'공부 > PS' 카테고리의 다른 글
| [BOJ] 1655: 가운데를 말해요 (0) | 2020.07.14 |
|---|---|
| [BOJ] 7453: 합이 0인 네 정수 (0) | 2020.07.12 |
| [BOJ] 4902: 삼각형의 값 (0) | 2020.07.11 |
| [BOJ] 16988: Baaaaaaaaaduk2 (Easy) (0) | 2020.07.09 |
| [BOJ] 17406: 배열 돌리기 4 (0) | 2020.07.06 |
